In Chap. 4 we learned to program the computer to make “decisions” by branching to different parts of a definition depending on the outcome of certain tests. Conditional branching is one of the things that make computers as useful as they are.
In this chapter, we’ll see how to write definitions in which execution can conditionally branch back to an earlier part of the same definition, so that some segment will repeat again and again. This type of control construct is called a “loop.” The ability to perform loops is probably the most significant thing that makes computers as powerful as they are. If we can program the computer to make out one payroll check, we can program it to make out a thousand of them.
For now we’ll write loops that do simple things like printing numbers at your terminal. In later chapters, we’ll learn to do much more with them.
On This Page
Definite Loops — DO…LOOP
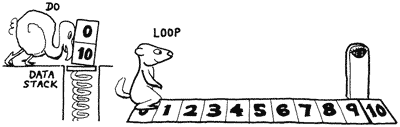
One type of loop structure is called a “definite loop.” You, the programmer, specify the number of times the loop will loop. In Forth, you do this by specifying a beginning number and an ending number (in reverse order) before the word DO. Then you put the words which you want to have repeated between the words DO and LOOP. For example
: TEST 10 0 DO CR ." Hello " LOOP ;
will print a carriage return and “Hello” ten times, because zero from ten is ten.
TEST Hello Hello Hello Hello Hello Hello Hello Hello Hello Hello ok
Like an IF…THEN statement, which also involves branching, a DO…LOOP statement must be contained within a (single) definition.
The ten is called the “limit” and the zero is called the “index.”
FORMULA: limit index DO ... LOOP
Here is what happens inside a DO…LOOP:
First DO puts the index and the limit on the loop control stack.
Then execution proceeds to the words inside the loop, up to the word LOOP.
LOOP adds one to the index. If the index is less than the limit, LOOP reroutes execution back to DO.
Eventually the index reaches ten, and LOOP lets execution move on to the next word in the definition.
The Forth word I copies the current loop index onto the parameter stack. You can use I to get hold of the current value of the index each time around. Consider the definition
: DECADE 10 0 DO I . LOOP ;
which executes like this:
DECADE ↵0 1 2 3 4 5 6 7 8 9 ok Of course, you could pick any range of numbers (within the range of -2147483648 to +2147483647):
: SAMPLE -243 -250 DO I . LOOP ;
SAMPLE ↵-250 -249 -248 -247 -246 -245 -244 ok
Notice that even negative numbers increase by one each time. The limit is always higher than the index.
You can leave a number on the stack to serve as an argument to something inside a DO loop. For instance,
: MULTIPLICATIONS CR 11 1 DO DUP I * . LOOP DROP ;
will produce the following results:
7 MULTIPLICATIONS↵ 7 14 21 28 35 42 49 56 63 70 ok Here we’re simply multiplying the current value of the index by seven each time around. Notice that we have to DUP the seven inside the loop so that a copy will be available each time and that we have to DROP it after we come out of the loop.
A compound interest problem gives us the opportunity to demonstrate some trickier stack manipulations inside a DO loop.
Given a starting balance, say $1000, and an interest rate, say 6%, let’s write a definition to compute and print a table like this:
1000 6 COMPOUND
YEAR 1 BALANCE 1060
YEAR 2 BALANCE 1124
YEAR 3 BALANCE 1191
etc.
for twenty years.
First we’ll load R%, our previously-defined word from Chap. 5, then we’ll define
: COMPOUND ( amount interest -- ) CR SWAP 21 1 DO ." YEAR " I . 3 SPACES 2DUP R% + DUP ." BALANCE " . CR LOOP 2DROP ;
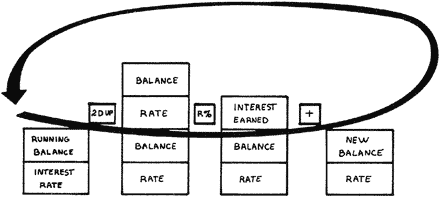
Each time through the loop, we do a 2DUP so that we always maintain a running balance and an unchanged interest rate for the next go-round. When we’re finally done, we 2DROP them.
Getting Iffy
The index can also serve as a condition for an IF statement. In this way you can make something special happen on certain passes through the loop but not on others. Here’s a simple example:
: RECTANGLE 256 0 DO I 16 MOD 0= IF CR THEN ." *" LOOP ;
RECTANGLE will print 256 stars, and at every sixteenth star it will also perform a carriage return at your terminal. The result should look like this:
****************
****************
****************
****************
****************
****************
****************
****************
****************
****************
****************
****************
****************
****************
****************
****************
And here’s an example from the world of nursery rhymes. We’ll let you figure this one out.
: POEM CR 11 1 DO I . ." Little "
I 3 MOD 0= IF ." indians " CR THEN
LOOP ." indian boys. " ;
Nested Loops
In the last section we defined a word called MULTIPLICATIONS, which contains a DO…LOOP. If we wanted to, we could put MULTIPLICATIONS inside another DO…LOOP, like this:
: TABLE CR 11 1 DO I MULTIPLICATIONS LOOP ;
Now we’ll get a multiplication table that looks like this:
1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 12 14 16 18 20 3 6 9 12 15 18 21 24 27 30 etc. 10 20 30 40 50 60 70 80 90 100
because the I in the outer loop supplies the argument for MULTIPLICATIONS.
You can also nest DO loops inside one another all in the same definition:
: TABLE CR 11 1 DO 11 1 DO I J * 5 U.R LOOP CR LOOP ;
Notice this phrase in the inner loop:
I J *
The Forth word J copies the next outer loop index onto the parameter stack. Thus the phrase “I J *” multiplies the two indices to create the value in the table.
Now what about this phrase?
5 U.R
This is nothing more than a fancy . that is used to print numbers in table form so that they line up vertically. The five represents the number of spaces we’ve decided each column in the table should be. The output of the new table will look like this:
1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 12 14 16 18 20 3 6 9 12 15 18 21 24 27 30 etc.
Each number takes five spaces, no matter how many digits it contains. (U.R stands for “unsigned number-print, right justified.” The term “unsigned,” you may recall, means you cannot use it for negative numbers.)
+LOOP
If you want the index to go up by some number other than one each time around, you can use the word +LOOP instead of LOOP. +LOOP expects on the stack the number by which you want the index to change. For example, in the definition
: PENTAJUMPS 50 0 DO I . 5 +LOOP ;
the index will go up by five each time, with this result:
PENTAJUMPS↵0 5 10 15 20 25 30 35 40 45 ok while in
: FALLING -10 0 DO I . -1 +LOOP ;
the index will go down by one each time, with this result:
FALLING↵0 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 ok
The argument for +LOOP, which is called the “increment,” can come from anywhere, but it must be put on the stack each time around. Consider this experimental example:
: INC-COUNT DO I . DUP +LOOP DROP ;
There is no increment inside the definition; instead, it will have to be on the stack when INC-COUNT is executed, along with the limit and index. Watch this:
Step up by one:
1 5 0 INC-COUNT↵0 1 2 3 4 ok Step up by two:
2 5 0 INC-COUNT↵0 2 4 ok Step down by three:
-3 -10 10 INC-COUNT↵10 7 4 1 -2 -5 -8 ok Our next example demonstrates an increment that changes each time through the loop.
: DOUBLING 32767 1 DO I . I +LOOP ;
Here the index itself is used as the increment (I +LOOP), so that starting with one, the index doubles each time, like this:
DOUBLING↵ 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192 16384 ok 
Notice that in this example we don’t ever want the argument for +LOOP to be zero, because if it were we’d never come out of the loop. We would have created what is known as an “infinite loop.”
DOing it — Forth Style
There are a few things to remember before you go off and write some DO loops of your own.
First, keep this simple guide in mind:
Reasons for Termination
Execution makes its exit from a loop when, in going up, the index has reached or passed the limit.
Or, when in going down, the index has passed the limit — not when it has merely reached it.
But a DO loop always executes at least once (this example will loop millions of times on a true ANS Forth system, so be prepared):
: TEST 100 10 DO I . -1 +LOOP ; TEST↵10 9 8 7 ... Second, remember that the words DO and LOOP are branching commands and that therefore they can only be executed inside a definition. This means that you cannot design/test your loop definitions in “calculator style” unless you simulate the loop yourself.
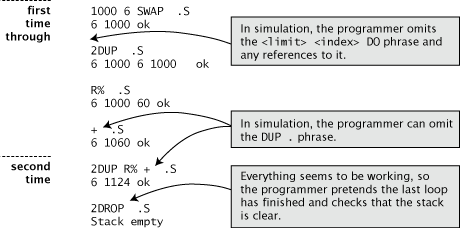
Let’s see how a fledgling Forth programmer might go about design/testing the definition of COMPOUND (from the first section of this chapter). Before adding the .” messages, the programmer might begin by jotting down this version on a piece of paper:
: COMPOUND ( amt int -- ) SWAP 21 1 DO I . 2DUP R% + DUP . CR LOOP 2DROP ;
The programmer might test this version at the terminal, using . or .S to check the result of each step. The “conversation” might look like this:
A Handy Hint: How to Clear the Stack
Sometimes a beginner will unwittingly write a loop which leaves a whole lot of numbers on the stack. For example
: FIVES 100 0 DO I 5 . LOOP ;
instead of
: FIVES 100 0 DO I 5 * . LOOP ;
If you see this happen to anyone (surely it will never happen to you!) and if you see the beginner typing in an endless succession of dots to clear the stack, recommend typing in
XX
XX is not a Forth word, so the text interpreter will execute the word ABORT”, which among other things clears all stacks. The beginner will be endlessly grateful.
Indefinite Loops
While DO loops are called definite loops, Forth also supports “indefinite” loops. This type of loop will repeat indefinitely or until some event occurs. A standard form of indefinite loop is
BEGIN ... UNTIL
The BEGIN…UNTIL loop repeats until a condition is “true.”
The usage is
BEGIN xxx f UNTIL
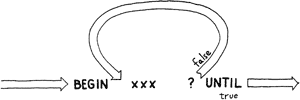
where “xxx” stands for the words that you want to be repeated, and “f” stands for a flag. As long as the flag is zero (false), the loop will continue to loop, but when the flag becomes non-zero (true), the loop will end.
An example of a definition that uses a BEGIN…UNTIL statement is one we mentioned earlier, in our washing machine example:
: TILL-FULL BEGIN ?FULL UNTIL ;
which we used in the higher-level definition
: FILL FAUCETS OPEN TILL-FULL FAUCETS CLOSE ;
?FULL will be defined to electronically check a switch in the washtub that indicates when the water reaches the correct level. It will return zero if the switch is not activated and a one if it is. TILL-FULL does nothing but repeatedly make this test over and over (millions of times per second) until the switch is finally activated, at which time execution will come out of the loop. Then the ; in TILL-FULL will return the flow of execution to the remaining words in FILL, and the water faucets will be turned off.
Sometimes a programmer will deliberately want to create an infinite loop. In Forth, the best way is with the form
BEGIN ... AGAIN
The word AGAIN branches back to the BEGIN unconditionally, so the loop will repeat eternally.
Beginners usually want to avoid infinite loops, because executing one means that they lose control of the computer (in the sense that only the words inside the loop are being executed). But infinite loops do have their uses. For instance, the text interpreter is part of an infinite loop called QUIT, which waits for input, interprets it, executes it, prints “ok,” then waits for input once again. In most microprocessor-controlled machines, the highest-level definition contains an infinite loop that defines the machine’s behavior.
Another form of indefinite loop is used in this format:
BEGIN xx f WHILE yyy REPEAT
Here the test occurs halfway through the loop rather than at the end. As long as the test is true, the flow of execution continues with the rest of the loop, then returns to the beginning again. If the test is false, the loop ends.
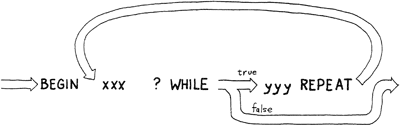
Notice that the effect of the test is opposite that in the BEGIN…UNTIL construction. Here the loop repeats while something is true (rather than until it’s true).
The indefinite loop structures lend themselves best to cases in which you’re waiting for some external event to happen, such as the closing of a switch or thermostat, or the setting of a flag by another part of an application that is running simultaneously. So for now, instead of giving examples, we just want you to remember that the indefinite loop structures exist.
The Indefinitely Definite Loop
There is a way to write a definite loop so that it stops short of the prescribed limit if a truth condition changes state, by using the word LEAVE. LEAVE causes the loop to end immediately.
Watch how we rewrite our earlier definition of COMPOUND. Instead of just letting the loop run twenty times, let’s get it to quit after twenty times or as soon as our money has doubled, whichever occurs first.
We’ll simply add this phrase:
2000 > IF LEAVE THEN
like this:
: DOUBLED
6 1000 21 1 DO CR ." YEAR " I 2 U.R
2DUP R% + DUP ." BALANCE " .
DUP 2000 > IF CR CR ." more than doubled in "
I . ." years " LEAVE THEN
LOOP 2DROP ;
The result will look like this:
DOUBLED
YEAR 1 BALANCE 1060
YEAR 2 BALANCE 1124
YEAR 3 BALANCE 1191
YEAR 4 BALANCE 1262
YEAR 5 BALANCE 1338
YEAR 6 BALANCE 1418
YEAR 7 BALANCE 1503
YEAR 8 BALANCE 1593
YEAR 9 BALANCE 1609
YEAR 10 BALANCE 1790
YEAR 11 BALANCE 1897
YEAR 12 BALANCE 2011
more than doubled in 12 years ok
One of the problems at the end of this chapter asks you to rework DOUBLED so that it expects the parameters of interest and starting balance, and computes by itself the double balance that LEAVE will try to reach.
Two Handy Hints: PAGE and QUIT
To give a neater appearance to your loop outputs (such as tables and geometric shapes), you might want to clear the screen first by using the word PAGE. You can execute PAGE interactively like this:
PAGE RECTANGLE
which will clear the screen before printing the rectangle that we defined earlier in this chapter. Or you could put PAGE at the beginning of the definition. like this:
: RECTANGLE PAGE 256 0 DO I 16 MOD
0= IF CR THEN ." *" LOOP ;
If you don’t want the “ok” to appear upon completion of execution, use the word QUIT. Again, you can use QUIT interactively:
RECTANGLE QUIT
or you can make QUIT the last word in the definition (just before the semicolon).
Chapter Summary
Forth Words
Here’s a glossary of the Forth words we’ve covered in this chapter:
- DO
- ( limit index — )
- Sets up a finite loop, given the index and limit. Usage:
DO ... LOOP DO ... n +LOOP
- LOOP
- ( — )
- Add one to the loop index. If the loop index is then equal to the loop limit, discard the loop parameters and continue execution immediately following LOOP. Otherwise continue execution at the beginning of the loop (after DO).
- +LOOP
- ( n — )
- Add n to the loop index. If the loop index did not cross the boundary between the loop limit minus one and the loop limit, continue execution at the beginning of the loop. Otherwise, discard the current loop control parameters and continue execution immediately following the loop (after DO).
- LEAVE
- ( — )
- Terminate the loop immediately.
- BEGIN
- ( — )
- Marks the start of an indefinite loop. Usage:
BEGIN ... flag UNTIL BEGIN ... flag WHILE ... REPEAT BEGIN ... AGAIN
- UNTIL
- ( flag — )
- If flag is false, go back to BEGIN. If flag is true, terminate the loop.
- WHILE
- ( flag — )
- If flag is true, continue. If flag is false, terminate the loop (after REPEAT).
- REPEAT
- ( — )
- Resolves forward branch from WHILE; goes back to BEGIN.
- AGAIN
- ( — )
- Go back to BEGIN (infinite loop).
- U.R
- ( u1 u2 — )
- Prints the unsigned single-length number u1, right-justified within the field width u2.
- PAGE
- ( — )
- Clears the terminal screen and resets the terminal’s cursor to the upper left-hand corner.
- QUIT
- ( — )
- Terminates execution for the current task and returns control to the terminal.
Review of Terms
- Definite loop
- a loop structure in which the words contained within the loop repeat a definite number of times. In Forth, this number depends on the starting and ending counts (index and limit) which are placed on the stack prior to the execution of the word DO.
- Infinite loop
- a loop structure in which the words contained within the loop continue to repeat without any chance of an external event stopping them, except for closing the Forth window or shutting down or resetting the computer.
- Indefinite loop
- a loop structure in which the words contained within the loop continue to repeat until some truth condition changes state (true-to-false or false-to-true). In Forth, the indefinite loops begin with the word BEGIN.

Problems — Chapter 6
In Problems 1 through 6, you will create several words which will print out patterns of stars (asterisks). These will involve the use of DO loops and BEGIN…UNTIL loops.
- First create a word named STARS which will print out n stars on the same line, given n on the stack:
10 STARS↵********** ok - Next define BOX which prints out a rectangle of stars, given the width and height (number of lines), using the stack order ( width height — ).
10 3 BOX
**********
**********
********** ok - Now create a word named \STARS which will print a skewed array of stars (a rhomboid), given the height on the stack. Use a DO loop and, for simplicity, make the width a constant ten stars.
3 \STARS
**********
**********
********** ok - Now create a word which slants the stars the other direction: call it /STARS. It should take the height as a stack input and use a constant ten width. Use a DO loop.
- Now redefine this last word, using a BEGIN…UNTIL loop.
- Write a definition called DIAMONDS which will print out the given number of diamond shapes, as shown in this example.
2 DIAMONDS
*
***
*****
*******
*********
***********
*************
***************
*****************
*******************
*******************
*****************
***************
*************
***********
*********
*******
*****
***
*
*
***
*****
*******
*********
***********
*************
***************
*****************
*******************
*******************
*****************
***************
*************
***********
*********
*******
*****
***
* - In our discussion of LEAVE we gave an example which computed 6% compound interest on a starting balance of $1000 for 20 years or until the balance had doubled, whichever came first. Rewrite this definition so that it will expect a starting balance and interest rate on the stack and will LEAVE when this starting balance has doubled.
- Define a word called ** that will compute exponential values, like this:
7 2 ** . 49 ok(seven squared)
2 4 ** . 16 ok(two to the fourth power). For simplicity, assume positive exponents only (but make sure ** works correctly when the exponent is one — the result should be the number itself).
Answers
: STAR [CHAR] * EMIT ; : STARS ( #stars -- ) 0 DO STAR LOOP ;
: BOX ( width height -- ) 0 DO CR DUP STARS LOOP DROP ;
: \STARS ( height -- ) 0 DO CR I SPACES 10 STARS LOOP ;
: /STARS ( height -- ) 1- 0 SWAP DO CR I SPACES 10 STARS -1 +LOOP ;
: A/STARS ( height -- ) BEGIN CR 1- DUP SPACES 10 STARS DUP 0= UNTIL DROP ;
: TRIANGLE ( increment limit start -- ) DO CR 9 I - SPACES I 2* 1+ STARS DUP +LOOP DROP ; : DIAMONDS ( #diamonds -- ) 0 DO 1 10 0 TRIANGLE -1 0 9 TRIANGLE LOOP ;
: R% ( n1 % -- n2 ) 10 */ 5 + 10 / ; : DOUBLED ( amount interest -- ) OVER 2* SWAP ROT 21 1 DO CR ." Year " I 2 .R 3 SPACES 2DUP R% + DUP ." Bal " . DUP 2OVER DROP > IF CR CR ." More than doubled in " I . ." years " LEAVE THEN LOOP 2DROP DROP ;: ** ( n1 n2 -- n1**n2 ) 1 SWAP ?DUP IF 0 DO OVER * LOOP THEN NIP ;
